---

---

---

---

unique visitors since March 2009

---

C3: Algebra and Functions

---

Simplifying Expressions

Algebra works just like arithmetic. What works with numbers must also work with algebra because the letters in algebra stand for numbers.

I felt the need to point this out because I have seen so many ridiculous mistakes with algebra that would never happen with numbers.

Here's a couple of exam questions on this stuff.

---

Functions

Up until now we have used the word "function" without a really strong (rigorous) understanding of what it means.

In C3 we shall look at what "function" means. We will see that sometimes we will need to restrict what numbers we allow into our function (so that we don't divide by zero, for instance) and how to find the inverse function.

We will also meet a new (and very simple) function: the modulus function. We wil look at graphs of functions, including our new function, and transformations of functions.

Function Definition

At primary school you will have met the idea of a function machine. This might have been a (pretend) box that you feed numbers into and get a number out the other side. As a really simple example a "+1" function machine simply takes your number (say, 5) and adds one to give you a new number, the output (for an input of 5, the output would be 6).

In this course (and earlier) you will have used f(x) to define a function. For example:

f(x) = x²

By the way, another way of writing this is

f : x → x², which is pronounced, "f maps x onto x².

An input of 3 gives an output of 9 (3²). We could write this in a much more "grown-up" way as:

f(3) = 9

Another example: suppose our function returned the reciprocal of the input. (remember that reciprocal means 1/x) I have already used "f" for the first function, so I'll call this one g(x).

g(x) = 1/x

And we could write g(2) = ½.

Now, what is g(0)?

Here we see a problem. It is mathematically illegal to divide by zero. Try to do this on a calculating machine and you'll get some sort of "math error"; do it in Excel and you'll get "#DIV0" or something like it. We must not allow the user of our function to try to input zero as it will cause an error. We do this by restricting what numbers are allowed in.

Domain and Range

In the above example we stop the function from blowing up (dividing by zero) by banning the user of our function from using zero as an input.

We write this as part of our function definition like this:

g(x) = 1/x, x ∈ ℜ, x ≠ 0

This is read as "g of x equals one over x, where x is a real number but not zero"

That strange symbol (ℜ,) just means that x can be any real number (3, 0.5, -45, π, √2 etc.). In other words any number. (In FP1 you will meet other numbers called imaginary numbers but we don't need to worry about those here). The bit which says "x ≠ 0" just makes it clear that zero is banned from our function.

Here is the square-root function.

h(x) = √x

I have allowed any number to be input into it. Can you spot the problem that this makes?

The square root function will cause an error if you try to input a negative value. You can't find the square root of -2 for example.

I have now written the full definition of the square root function to avoid any errors:

h(x) = √x, x ∈ ℜ, x ≥ 0.

That should guarantee that no negative numbers get in to our machine causing problems.

In the h(x) function definition we banned negative numbers. But why stop there? It's our function, so we can decide what to allow in. We could make sure that only numbers between 3 and 6 are allowed in like this:

h(x) = √x, x ∈ ℜ, 3 < x < 6.

The numbers that are allowed in to our function are called the domain of the function. Usually the domain of a function is all real numbers but sometimes we must ban certain inputs (to avoid breaking math laws like division by zero or square-rooting negatives) and sometimes we ban some inputs for other reasons (such as we are only interested in certain input-output pairs.)

Look back at our f(x) function (I have added the domain):

f(x) = x², x ∈ ℜ

What number went in if the output was 9?

The input must've been either -3 or +3 as both (-3)² and 3² are equal to 9.

What number must've gone in if the output was -4?

No matter what numbers we try to input in to the machine, we cannot seem to get -4 as the output. This is because no number multiplied by itself gives a negative result. The answer to the question is that you can't get -4 as the output. The question does not make sense.

Hopefully you see that the f(x) function only outputs certain values. In fact we can get any non-negative number out.

We could say this much more clearly:

f(x) = x², x ∈ ℜ

⇒ f(x) ≥ 0

This last line tells us what values can possibly be output by the function. These values are called the range of the function.

So the domain is all the values allowed in and the range is all the values we can get out.

Here's a function I ahve just invented. See if you can tell what the domain and range are for my function.

k(x) = x + 1, x ∈ ℜ, 0 ≤ x ≤ 4.

The domain of the function is given in the definition. My function will allow any real number between zero and four in (including zero and four). My function thakes the input and adds one. This means that the smallest output is one and the largest output is five. The range of my function is therefore: f(x) is between 1 and 4 inclusive.

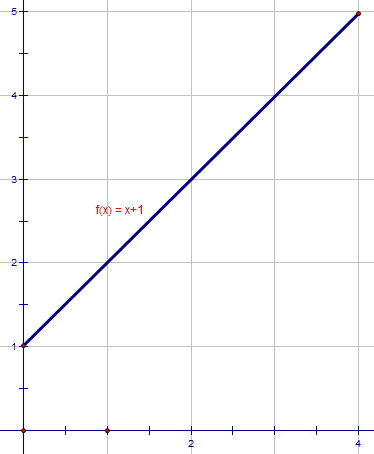
Here is a graph of my function. Notice that no x values exist below zero or above four because I have banned them. The x values that are allowed are called the domain.

The y-values on the graph go from 1 to 5. This is the range.

So the x-values are the domain and the y-values are the range.

Inverse Functions

If a function maps x to f(x), then the inverse function gets you back to x again.

eg. These are inverse functions

f : x → x + 1

f ^-1: x → x - 1.

because if you feed 9 into f, you get 10. Feeding 10 into f ^-1 gets you back to 9. Try it with other numbers.

Here are some other functions and their inverses.

Function f (x)	Inverse Function f -1(x)
x + 6	x - 6
6x	x/6
2x + 1	½ (x - 1)
¼x + 2	4(x - 2)

And now for a guessing game...

I am thinking of a number. I feed my number into the function f : x → x² and my answer is 4.

Can you guess my number?

Are you absolutely certain?

Hopefully you see the simple point I am trying to make, namely that my number might be either 2 or -2 and there's no way of knowing. These type of functions (where different inputs give the same output) are called "many to one" because many numbers (okay 2 different numbers in this case) give just one answer.

Functions like this can't have an inverse because there is no way of being certain that we get back to the original number.

A function that has only one possible answer for each question and only one question for each answer is called a one-to-one function

So squaring has no inverse since both 2 squared and (-2) squared both have the same answer. You should remember that trig functions also behave like this: sin30, sin150, sin390, sin510,... are all 0.5.

You are now sat there saying to yourself, "what is he on about? Of course there's an inverse of x² and it's √x." Well not according to what I've just said.

For f (x = x² to have an inverse we need to make sure that we don't get the same output for two different inputs. How can we do this?

EASY!!! We just restrict the numbers that we allow in! Play this guessing game: I'm thinking of a *positive* number. When I square it the answer is 4, what's my number? Are you sure? See how insisting that I only play with positive numbers makes this a one-to-on function, and so it can have an inverse, square-root.

If it exists, it's quite easy to figure out the inverse of a function. Simply think of your function as x = f (y) and make y the subject as in this example

eg Find the inverse of the following function.

f : x → x² - 10, x ∈ ℜ, x ≥ 0

Answer

Let x = y² - 10.

Re-arranging gives y = √(x + 10)

The possible outputs of f (x) (the RANGE) become the inputs of the inverse function (its DOMAIN). So the domain of the inverse is all numbers ≥ -10 since any number from -10 upwards can be outputted from our function. The inverse function is therefore:

f ^-1: x → √(x + 10), x ∈ ℜ, x ≥ -10

I attempt to explain this in the following clip...

The Modulus Function

We already know some easy functions from ages ago: x + 4, x ÷ 8. Later we learned so trickier ones: x², √x. Then we met some even tougher functions: sin x, log x.

Well, now it's time for a new one. The modulus function. This function is in the easy catagory - all it does is make the input non-negative by simply ignoring the minus sign if there is one, or doing nothing if there isn't.

And that's it.

The modulus function is written |x|

We could add a domain to our function definition:

f(x) = |x|, x ∈ ℜ

And so f(3) = 3, f(66) = 66, f(-36) = 36, f(-356) = 356, f(0) = 0 etc.

Can you figure out the range of f(x)?

Any number is allowed into our function, but the modulus function ignores minus signs when it gives you the output. It is impossible to output -2 for instance. This means only numbers graeter than or equal to zero can be output. The range is therefore f(x)>=0, where ">=" means "greater than or equal to" (I can't use the correct symbol for this in a text box).

Here's a graph of the modulus function.

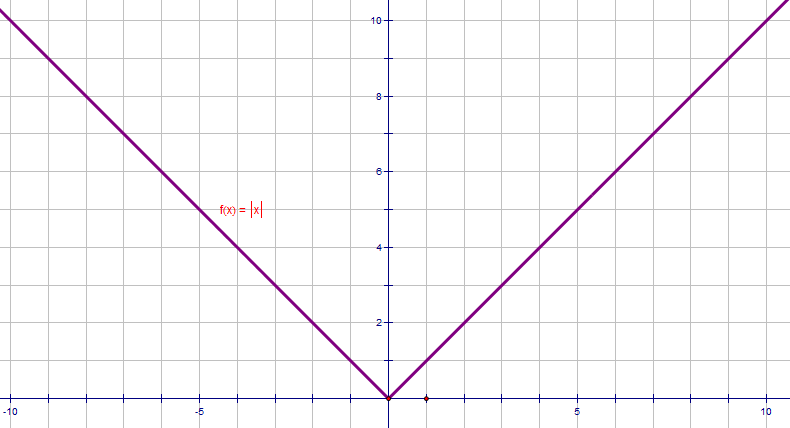
Hopefully you can see that x (domain) can take any value, whilst y (range) is never negative.

---

Combinations of Transformations