---

---

---

---

unique visitors since March 2009

---

C3: Exponentials & Logarithms

---

We last met logarithms in C2, where we established a few laws or rules for manipulating them.

There's good news and there's ace news about C3's logarithms. The good news is that there is nothing new. We will use the same rules for C3 as for C2, the only difference is that we will use a special base for our logarithms that we have not yet seen. This base will be so special that it gets its own symbol and its own button on a calculating machine.

And that's the ace news: the base we will be using is such a special number that it crops up in loads of areas of maths. The more I learn about mathematics, the more uses there seem to be for the number.

Before going on, try this: half-a-Twix to anyone who can draw a graph of a function where the gradient of the function is the same as the value of the function (ie the y-coordinate.

There are three ways in which this can be done. The first, and most obvious, is the x-axis itself. On the x-axis the y coordinate is always zero and the gradient is always zero - so the gradient is always the same as the function. The other two should look like exponential funcions from C2 - so y = a^x is the answer. But what is a?

If you look at the graph of y = 2^x you should see that it looks like it might be the function we're after.

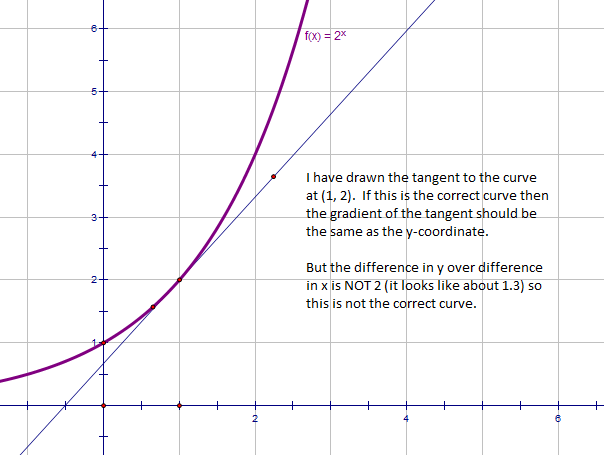
It looks as though y = 2^x is not steep enough. If it was correct, then my tangent would pass through the origin. Lets look at y = 3^x next.

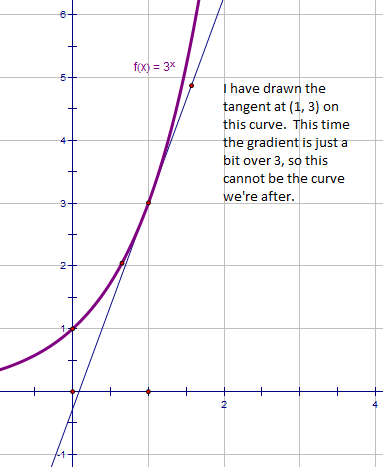
Not bad! But this time the curve is too steep. Somewhere between 2^x and 3^x is our magical function

It turns out that y = 2.7183^x is very close to the function we seek. This number is going to be really important later. We shall call it "e" - the exponential function.

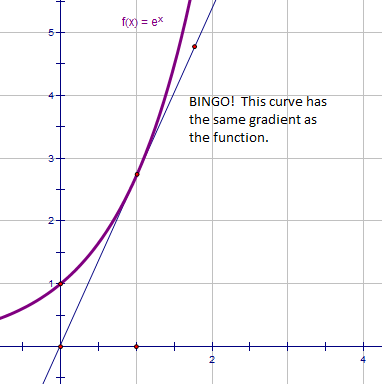
So this curve always has the same gradient as the value of the function (gradient = y-coordinate). This means that if we differentiate then dy/dx must be the same as y.

If y = e^x then dy/dx = e^x. We have found a function that is unaffected by calculus!

Let's have a look at a video clip of some exam questions.