C3: Numerical Methods
Ever since you first started to solve equations, there have always been some which (at the time) seem impossible.
Back in Y7 quadratics seemed like something that only a genius could solve. In Year 8 or Year 9 you probably learned a way to "solve" an equation such as x2 + 2x = 7. This method was called trial and improvement.
To solve an equation by trial and improvement, we "guess" where the solution is and test it to see how close we are. Then we have another guess, this time slightly bigger if our original guess was too small, or slightly smaller if our original was too big. It's a bit like Goldilocks testing porridge.
We eventually get a quite accurate approximation of the real solution.
The big problem with trial and improvement is that it is slow to get to the approximate solution. At A-Level we require a much faster way to solve those equations that we cannot solve using normal algebraic methods. We will never find accurate solutions to these type of equations if they're irrational - we are finding approximations only.
We will see that we can find answers to 8 decimal places very quickly using the Numerical Methods described below.
Location of Roots
The first stage of finding the root of an equation such as x3 + 2x - 15 = 0 is to figure out where the solution is roughly. (I say "...solution is" although there may be more than one root - in this case there may be as many as 3 solutions as it's a cubic but we can only find one at a time).
We locate the root in just the same way as a Year 9 trial and improvement technique.
| Guess | Calculation | Comment |
| 2 | 23+2(2)-15=-3 | too small |
| 3 | 33+2(3)-15=18 | too big |
So, 2 is too small and 3 is too big. We conclude that a solution is somewhere between 2 and 3.
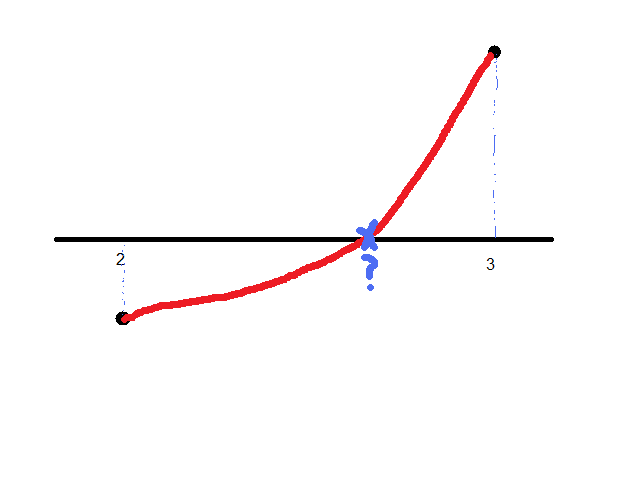
All that we are looking for is that for one value it works out to be positive, for the other it's negative. It doesn't matter which way round the positive and negative are (try to imagine this) - all we care about is that there is a change of sign.
Usually we won't be expected to guess where the root is ourselves. We will be asked to show that the root lies between two values which we will be told.
eg. Show that a root of the equation x3 - 30 = 0 lies between x = 3 and x = 4.
Solution:
f(3) = -3
f(4) = 34
Change of sign ⇒ root between 3 and 4.
Using Iteration Method to Find a Root
this is hard to explain with text so I'll make a clip...
In this clip I show you how to use a scientific calculating machine to get to the root really fast.
Watch out for my mistake near the end. Can you see where I went wrong?
Next time I do a "live" clip like this I'll make sure the light's right. Soz.

