D1: Linear Programming
Linear Programming is the area of mathematics that is all about finding the optimal solution to a problem (such as the most profit) with certain restrictions (called constraints).
The linear bit comes from the fact that the constaints will all be linear inequalities.
eg. Maximise P = 3x + y subject to the following constraints.
- x + y < 10
- 4x + y < 18
- x > 0
- x > 0
The last two constraints are called non-negativity constraints. You will always see these at this level (there will be no negative numbers). This is obvious when we start to give meaning to the variables later.
The first step is to draw a graph of these inequalities.
At GCSE you probably shaded the bit you wanted. Now you should shade out the bit that you don't want. The reason is that we will look to see which coordinates satisfy all of the inequalities and it is easier to see what hasn't been shaded at all that what has been shaded in 4 times.
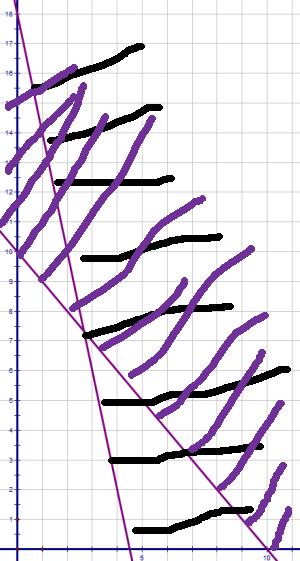
All possible solutions are in the unshaded bit.
But which is the best?
We are trying to maximise profit. We are told that P = 3x + y
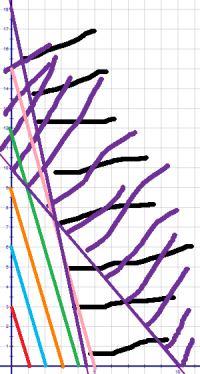
In this graph I have drawn the lines
P = 3 (red)
P = 6 (blue)
P = 9 (orange)
P = 12 (green)
P = 15 (pink)
These lines are all parallel to one another. The best profit is the pink line.
If I drew another line it would be outside the unshaded bit (this bit is called the feasible region as it contains all possible solutions.)
This gives us the name for the first method for finding the best solution. The ruler method...
Ruler Method
- Draw and shade the inequalities
- Draw any profit line. Choose an easy number - 3x + y = 4 would be daft as it's got awkward numbers
- Slide your ruler parallel to this line until you get to the very extreme of the feasible region
- That's it! You have the optimal solution. Read off the x and y values and calculate the value of P.
Vertex Method
You should have noticed that the ruler method will always end up and the intersection between 2 lines of your graph.
In other words, if we knew the value of P at each vertex then all we'd have to do is to choose the the biggest one.
The vertex method works by doing just that.
- Draw and shade the inequalities
- Find out the vertices of the feasible region. You might have to solve simple-taneous equations
- For each vertex, substitute the x and y values into the profit equation
- The highest value wins!
That's all very well but what if the vertex that wins does not have integer values?
What If The Winning Vertex Isn't Whole Numbers?
In case you haven't worked it out, the example above gave fractions as the answer.
The coordinates are (8/3, 22/3)
Often we will need integer solutions as the linear programming problem will usually involve things like the number of books or something like this.
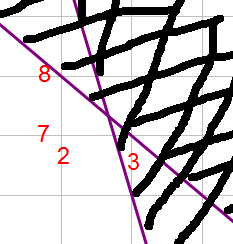
I have enlarged the graph around this vertex. We now look at the valid coordinates around this point.
There are four to consider:
- (2, 7) P = 3x + y = 13
- (3, 7) P = 3x + y = 16, but this point is outside the feasible region
- (2, 8) P = 3x + y = 14, but is this point valid?
- (3, 8) Not worth calculating as it's clearly outside the feasible region
So is (2, 8) feasible?
Just check that these numbers satisfy the inequalities...
- x + y < 10... NOPE it's not less than 10 as 2 + 8 equals 10
- 4x + y < 18... fine
- x > 0... fine
- x > 0... fine
So (2, 8) is no good and our best solution is at (2, 7) where P = 13.
Coming Soon... when my interweb connection's more betterer, I'll do a video of this stuff.
And here it comes...

