M1: Dynamics
If something is dynamic then it is constantly changing.
Forces
In a minute we'll see that Newton's Law explains all we need about why a particle's motion would be constantly changing. It's because the forces aren't balanced.
Newton's Law of Motion
Newton said An object's motion dunt change unless summat meks it
. What he meant was that if forces don't balance then there will be an
acceleration. His equation sums this up as F = ma. We shall use this equation in every Dynamic situation.
Connected Particles
We will meet 2 situations which we can model as two particles connected by a light inextensible string. The first is a car towing a caravan, or something similar. The second involves pulleys. In both situations a diagram is absolutely vital. In fact I reckon that the diagram is the most time-consuming part of the question.
I always draw the diagram with the motion going from left to right. Draw in the tow bar that connects the two objects. If they are moving on flat ground then the weight is not important as it is just balanced by the normal reaction. The mass is very important - I always draw the vehicles as oblongs with the mass inside
The tension in the rope/towbar is pulling the vehicle that's behind (so the arrow is forward) but slowing the vehicle in front (so the arrow is backwards). Of course the same force that slows one vehicle down is also pulling the other forward, so both forces are the same. In this diagram a car of mass 1000kg is towing a trailer of mass 600kg

The car will usually have a driving force - the force that makes the car move forward. Here the force is 1000 Newtons.

Finally, there is usually some sort of force slowing the vehicles down, friction usually (but it could be brakes or something). The friction forces is usually different for each vehicle, let's say friction is 400 N for the trailer and 600 N for the car...

Now we usually apply Newton's Law (F = ma) to each vehicle. I've done a clip of an exam question to show my technique.
Pulleys
Pulleys are the second type of connected particles. As with cars/trailers the important thing is a good, clear diagram. Then you usually just use Newton's Law. Occasionally a question involves the string snapping or one particle hitting the floor, making the string go slack. When this happens, the question goes into a second phase where the string makes no difference - it becomes a Kinematics question. Think carefully about what is being described in the question - these can get a bit tricky.
When Things Hit The Ground
As mentioned above, if a particle hits the ground (or the string brakes) we treat the question as a kinematics one. Here is an example from an exam.
Up/Down A Plane
Whenever something is moving up or down a plane we need an accurate diagram to start with. A few tips...
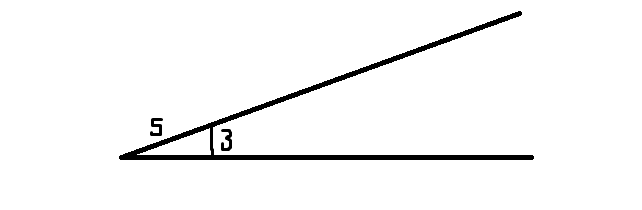
- If you're told the angle - write it in. If you're told something like sin θ = 3/5 DO NOT work out the angle. Draw a triangle in the
bottom corner with the numbers in the right place. In this example, sine is opposite/hypotenuse so I write the numbers in the positions as shown below.
I can calculate adjacent using knowledge of Pythagoras' Theorem (it will always be an integer in these questions - it's 4 in the one below).
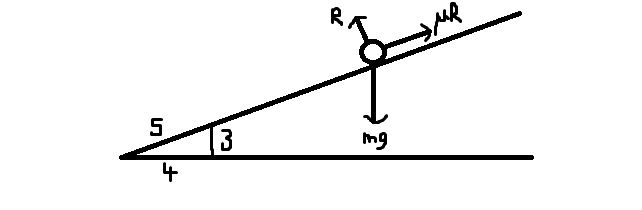
- Add all the forces. This will include weight, the normal reaction (always normal or perpendicular to the
plane, perhaps other forces such as friction. Friction always opposes motion and has a maximum value of μR,
where μ is the coefficient of friction and R is the normal reaction.
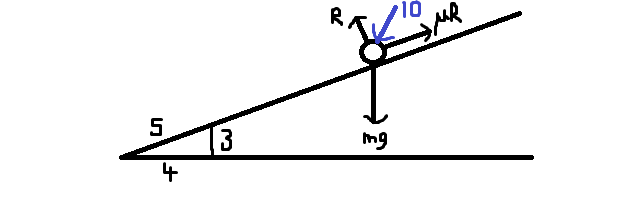
- I like to change any pushing force into a pulling force. I just prefer all arrows to come out of the particle rather than push into it.
In the diagram below, I have added a pushing force of 10 Newtons - I change this to a pulling force in the second diagram.
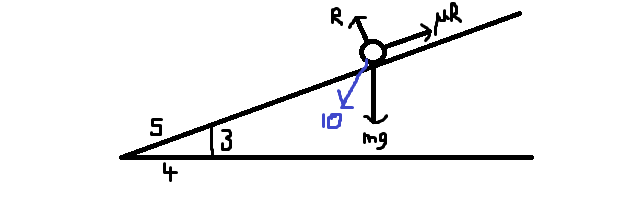
Of course I'd add the angle as well. - The next thing to do is almost always to resolve forces perpendicular to the plane to find the normal reaction. Forces will balance in this direction as there is no movement. If the only forces are weight, reaction and friction then we have mgcos θ = R. Of course we need to include the blue force for the situation above.
- Now use Newton's Law in the direction of motion (down the plane in our example). Friction is at its maximum when the object is moving.
Momentum & Impulse
We often use mathematical terms like force, power, energy, momentum and so on in imprecise ways in everyday talk.
Momentum is a measure of how much force is needed to change something's motion. Heavy, fast moving objects are the hardest to stop and so they have the most momentum. The calculation is simple
Momentum = mass × velocity
Like most things in mechanics, momentum is a vector - it has direction. Think about it, it needs a different force to stop a train that's travelling towards you than one running away.
The amazing thing about momentum is that it is not lost when particles collide. All that happens is that one particle gives some of its momentum to the other. This transfer of momentum is called impulse.
eg. Two 1 kg balls are travelling towards each other. The one on the left has speed 2 ms-1, whilst the other one has speed 1 ms-1. After the collision the one on the left stops. Find the speed of the one on the right.
Always draw diagrams for these situations
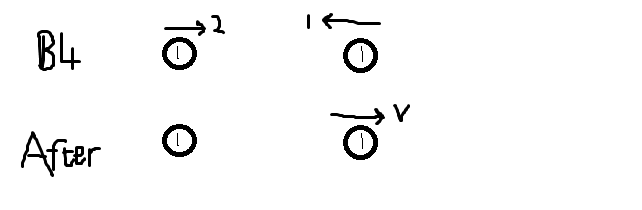
Note that the second particle has changed direction. How do I know this? Simple - it can't go left any more because the other particle would stop it. Now for the calculations...
Total momentum = (1 × 2) + (1 × -1)
Total momentum = 1 Ns (to the right)
A couple of points: I used minus one for the velocity of the right particle as it is travelling in the opposite direction; secondly the units of momentum are Newton-seconds. This is odd. Because momentum is mass × velocity, its units should be kilograms × metres per second. But wait! Newtons (unit of force) are equal to kilograms × metres per second per second. You do the math, as they say in the former colonies.
Friction
When stuff is moving, friction will do its best to slow down the acceleration. But there is only so much that friction can do. The maximum amount of friction is μR. Friction will always be in the oppposite direction to velocity. If there is no velocity (see Statics) then friction is in the opposite direction to what velocity would be, were there to be no friction.

