M1: Moments
Moments are turning forces. To get a feel of what this means go to your nearest door. Open the door wide and push it shut. That didn't take much effort did it? Now repeat the open/close door process but this time you must push the door near the hinge rather than the usual place near the handle. What do you notice?
The reason for this is that the turning force depends not only on how hard you push (force) but also how far away from the hinge you push (distance). The equation is simple:
Turning Force = Force × distance
We will restrict ourselves to looking only at turning forces applied to rods. There are two main situations that we will look at: firstly a rod balanced on one support (like a see-saw) and secondly a rod balanced on two supports. Both situations require a correct diagram and some careful thought before doing the sums.
One Support
These are easy! If a see-saw is to remain in equilibrium, the clockwise moments must balance the anticlockwise moments.
eg A hefty bloke is on a sew-saw with his wife. The bloke weighs in at 100kg whist his missus is only 60kg. If she sits on the end of her side, 3 metres from the centre, where should he sit?
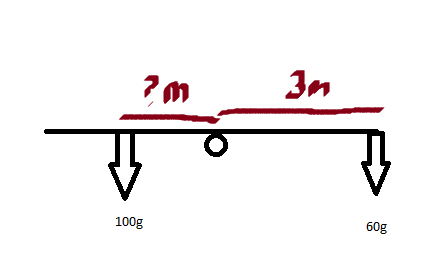
The clockwise force must balance the anticlockwise force. So
100g × x = 60g × 3, where x is the distance we're after. Solving gives:
x = 1.8m, which sounds about right.
Two Supports
You may have noticed that I didn't put the normal reaction on the support in the previous example. This is because it didn't really matter. When we have two supports, it is essential that we add normal reactions and the weight of the rod to our diagram. One more thing: remember that the turning force equals force multiplied by distance.
Tell you what, I'll do a few exam question to demonstrate. Get the following exams in front of you and read the moments questions...
You'll need Jan 2001, Jan 2008 and Jan 2002.

